微分と積分ってなに？ （概念理解とsympy）

微分と積分ってなに？

文系の自分は、高校の途中でアメリカをフラフラしていたこともあり、
微積分は知識ゼロだったため、社会人になってから改めて始めから勉強

細かい公式などは、ググるか、python先生に計算をお任せできるけど、
文系人間には概念の理解が難しかったのでメモ

概念

「微分」は「傾き」、「積分」は「面積」を出すこと

例えば、
「距離」を「時間（一定の変化率）」で微分すると「速さ」が出る
「速さ」を「時間（一定の変化率）」で積分すると「距離」が出る

微分

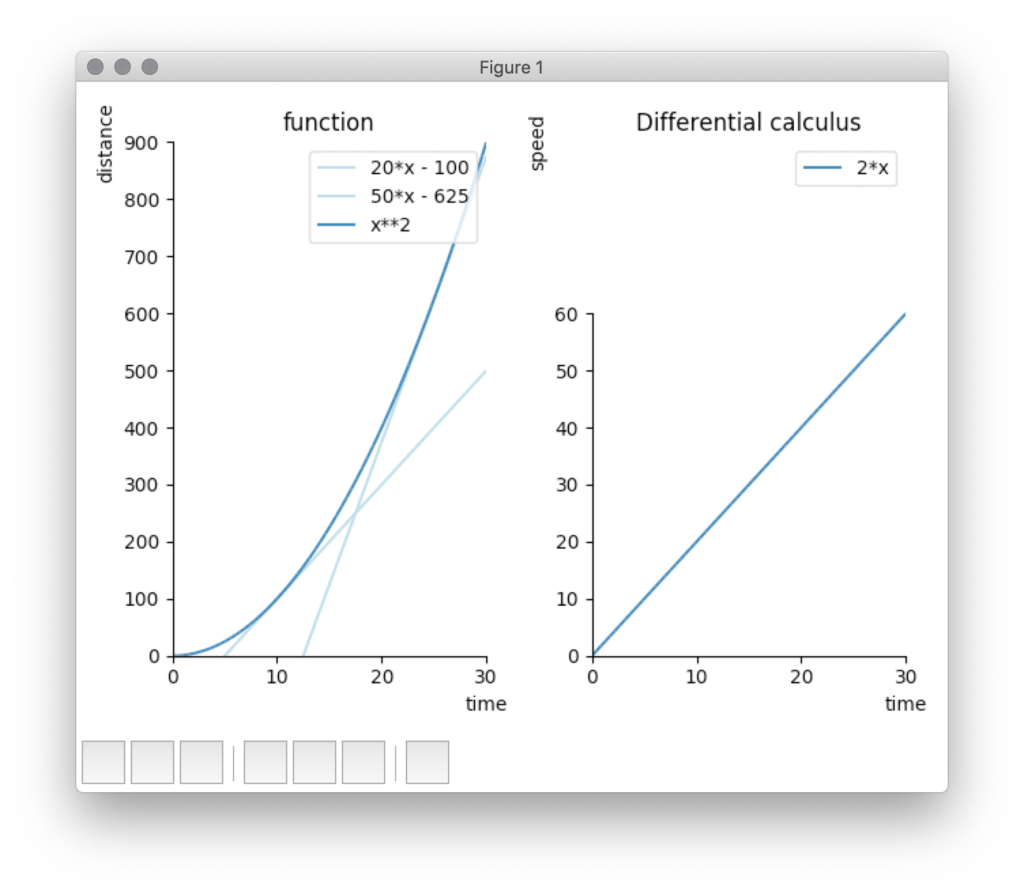
例えば、距離を表しているグラフ「x **2」を「微分」する
※ 以下グラフ「function」青線
※「 **2」は二乗の意味

接線を引いてみると、時間が大きくなるほど、傾きが大きくなることがわかる
※ 以下グラフ「function」水色線

つまり、微分すると右（「Differential calculus」）のようなグラフとなり、
どんどん傾き（スピード）を大きくなっていることがわかる
※ 以下グラフ「Differential calculus」

参考まで、グラフ表示のpythonコードは以下
※実行方法など詳細は、sympyを使って微分積分した結果をグラフにplotする を参照ください

% cat bibun_work.py
import sympy as sp
import matplotlib.pyplot as plt

if __name__ == '__main__':
  x = sp.symbols('x')   # 変数定義
  f_org = x **2   # 「x **2」の式を「f_org」とおく
  f_diff = sp.diff(f_org, x)   # 「f_org」の式を「x（時間）」微分する
  f_tlt_1 = 20 * x - 100   # 接線１
  f_tlt_2 = 50 * x - 625   # 接線２

  # 「function」のグラフ作成
  p1 = sp.plot(f_tlt_1, f_tlt_2, f_org, (x,0,30), ylim = [0,900], legend = True, show = False, xlabel = "time", ylabel = "distance", title = "function")

  p1[0].line_color = "lightblue"
  p1[1].line_color = "lightblue"

  # 「Differential calculus」のグラフ作成
  p2 = sp.plot(f_diff, (x,0,30), ylim = [0,90], legend = True, show = False, xlabel = "time", ylabel = "speed", title = "Differential calculus")

  # グラフ表示
  p = sp.plotting.PlotGrid(1, 2, p1, p2, legend = True, show = False)
  p.show()

積分

次は積分

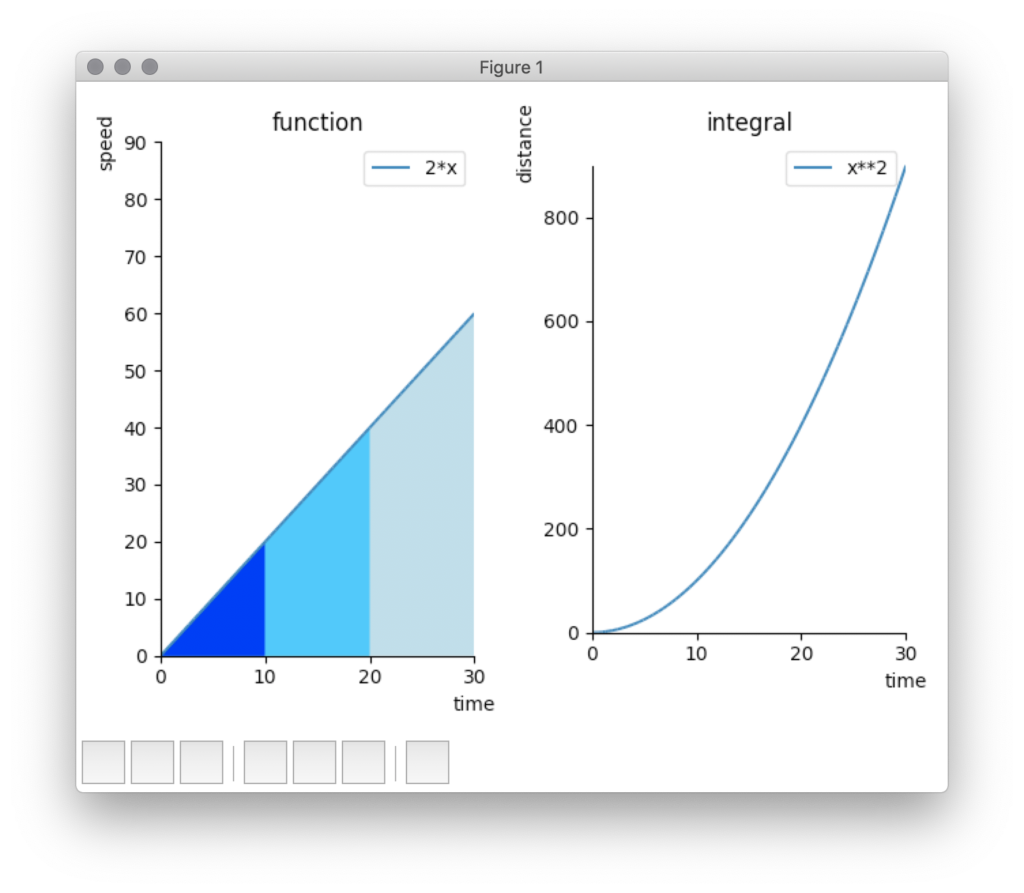
例えば、速さを表しているグラフ「2*x」を「積分」する
※ 以下グラフ「function」青線

xが大きくなるにつれて、「y=0」との面積は大きくなることがわかる
※ x=10までの面積（濃い青エリア）
※ x=20までの面積（濃い青エリア+水色エリア）
※ x=30までの面積（濃い青エリア+水色エリア+薄い水色エリア）

つまり、積分すると右（「integral」）のようなグラフとなり、
どんどん面積（距離）を大きくなっていることがわかる
※ 以下グラフ「integral」

参考まで、グラフ表示のpythonコードは以下
※実行方法など詳細は、sympyを使って微分積分した結果をグラフにplotする を参照ください

% cat sekibun_work.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-

import sympy as sp

if __name__ == '__main__':
  x,y = sp.symbols('x,y')   # 変数定義
  f_org = x * 2   # 「x *2」の式を「f_org」とおく
  f_inte = sp.integrate(f_org, x)   # 「f_org」の式を「x（時間）」で積分する
  f_inpl_1 = sp.And(2 * x > y, x < 10)   # xが10までの面積を「f_inpl_1」とおく
  f_inpl_2 = sp.And(2 * x > y, x < 20)   # xが20までの面積を「f_inpl_2」とおく
  f_inpl_3 = sp.And(2 * x > y, x < 30)   # xが30までの面積を「f_inpl_3」とおく

  # 「function」のグラフ作成
  p1 = sp.plot(f_org, (x,0,30), lylim = [0,90], show = False, xlabel = "time", ylabel = "speed")
  p2 = sp.plot_implicit(f_inpl_1, (x,0,30), (y,0,90), show = False, xlabel = "time", ylabel = "speed", line_color = "blue")
  p3 = sp.plot_implicit(f_inpl_2, (x,0,30), (y,0,90), show = False, xlabel = "time", ylabel = "speed", line_color = "deepskyblue")
  p4 = sp.plot_implicit(f_inpl_3, (x,0,30), (y,0,90), legend = True, show = False, xlabel = "time", ylabel = "speed", line_color = "lightblue", title = "function")
  p4.extend(p3)   # p4のグラフにp3のグラフを合成
  p4.extend(p2)   # p4のグラフにp2のグラフを合成
  p4.extend(p1)   # p4のグラフにp1のグラフを合成

  # 「integral」のグラフ作成
  p5 = sp.plot(f_inte, (x,0,30), lylim = [0,90], legend = True, show = False, xlabel = "time", ylabel = "distance", title = "integral")

  # グラフ表示
  p = sp.plotting.PlotGrid(1, 2, p4, p5, egend = True, show = False)
  p.show()

まとめ

上の例のように、単純なグラフなら微分積分を使わずに傾きや面積が出せるかもしれないが
以下のようなぐにゃぐにゃ曲がったグラフだと、計算が大変なので微分積分を使うことになる

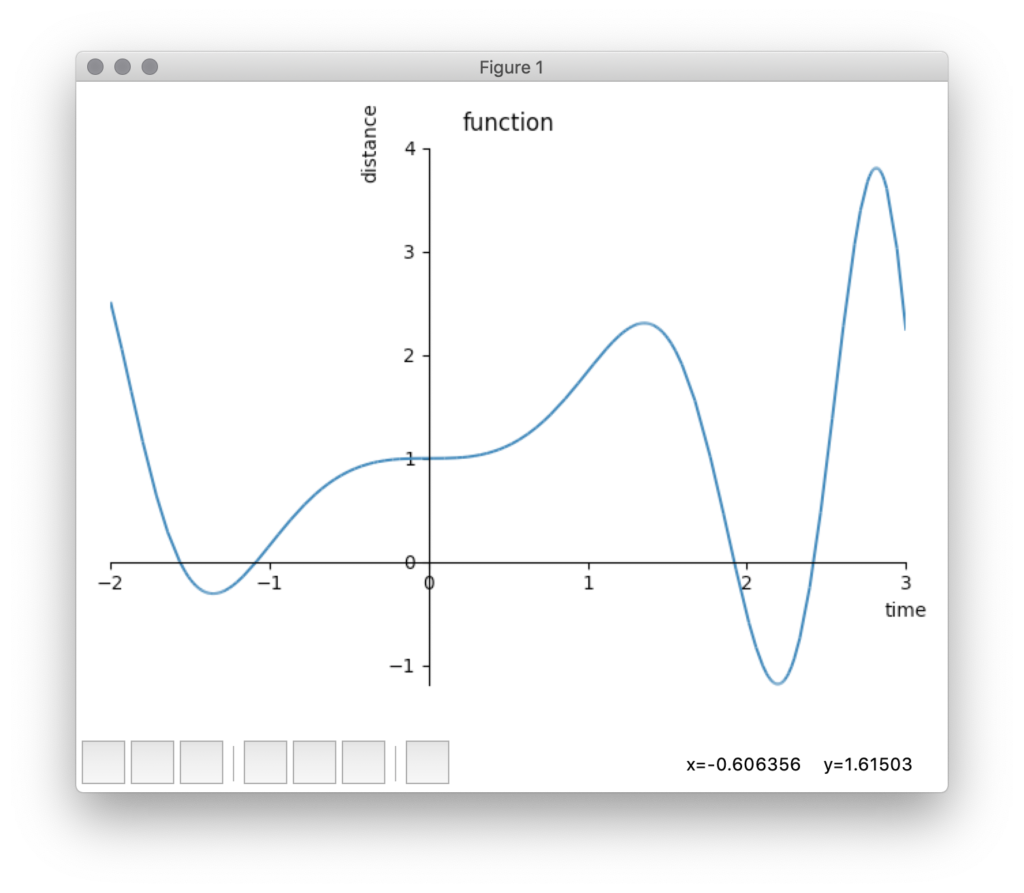
基本的な概念はここまで